diff 算法
核心逻辑
patchChildren 的方法,该方法的主要作用是为了 更新子节点,即:为子节点打补丁。
子节点的类型多种多样,如果两个 ELEMENT 的子节点都是 TEXT_CHILDREN 的话,那么直接通过 setText 附新值即可。
但是如果 新旧 ELEMENT 的子节点都为 ARRAY_CHILDREN 的话,那么想要完成一个 高效 的更新就会比较复杂了。这个时候,我们就需要,比较两组子节点,以达到一个高效的更新功能。这种 比较的算法 就是 diff 算法。
vue 中对 diff 算法的描述在 packages/runtime-core/src/renderer.ts 的 patchKeyedChildren(1759行) 方法中,观察该方法,可以发现该方法内部被分成了 5 块( 5 种场景):
sync from start:自前向后的对比sync from end:自后向前的对比common sequence + mount:新节点多于旧节点,需要挂载common sequence + unmount:旧节点多于新节点,需要卸载unknown sequence:乱序
常规场景
一、自前向后的diff对比
只有 vnode 的 key 和 type 都相同,才是 isSameVNodeType
// 1. 自前向后的 diff 对比。经过该循环之后,从前开始的相同 vnode 将被处理
while (i <= oldChildrenEnd && i <= newChildrenEnd) {
const oldVNode = oldChildren[i]
const newVNode = normalizeVNode(newChildren[i])
// 如果 oldVNode 和 newVNode 被认为是同一个 vnode,则直接 patch 即可
if (isSameVNodeType(oldVNode, newVNode)) {
patch(oldVNode, newVNode, container, null)
}
// 如果不被认为是同一个 vnode,则直接跳出循环
else {
break
}
// 下标自增
i++// 1. 自前向后的 diff 对比。经过该循环之后,从前开始的相同 vnode 将被处理
while (i <= oldChildrenEnd && i <= newChildrenEnd) {
const oldVNode = oldChildren[i]
const newVNode = normalizeVNode(newChildren[i])
// 如果 oldVNode 和 newVNode 被认为是同一个 vnode,则直接 patch 即可
if (isSameVNodeType(oldVNode, newVNode)) {
patch(oldVNode, newVNode, container, null)
}
// 如果不被认为是同一个 vnode,则直接跳出循环
else {
break
}
// 下标自增
i++二、自后向前的diff对比
// 2. 自后向前的 diff 对比。经过该循环之后,从后开始的相同 vnode 将被处理
while (i <= oldChildrenEnd && i <= newChildrenEnd) {
const oldVNode = oldChildren[oldChildrenEnd]
const newVNode = normalizeVNode(newChildren[newChildrenEnd])
if (isSameVNodeType(oldVNode, newVNode)) {
patch(oldVNode, newVNode, container, null)
} else {
break
}
oldChildrenEnd--
newChildrenEnd--
}// 2. 自后向前的 diff 对比。经过该循环之后,从后开始的相同 vnode 将被处理
while (i <= oldChildrenEnd && i <= newChildrenEnd) {
const oldVNode = oldChildren[oldChildrenEnd]
const newVNode = normalizeVNode(newChildren[newChildrenEnd])
if (isSameVNodeType(oldVNode, newVNode)) {
patch(oldVNode, newVNode, container, null)
} else {
break
}
oldChildrenEnd--
newChildrenEnd--
}经过第一步和第二步,此时新旧孩子的前面相同vnode和后面相同vnode已经处理好了
三、新节点多于旧节点时的 diff 比对
// 3. 新节点多余旧节点时的 diff 比对。
if (i > oldChildrenEnd) {
if (i <= newChildrenEnd) {
const nextPos = newChildrenEnd + 1
const anchor =
nextPos < newChildrenLength
? newChildren[nextPos].el
: parentAnchor
while (i <= newChildrenEnd) {
patch(
null,
normalizeVNode(newChildren[i]),
container,
anchor
)
i++
}
}
}// 3. 新节点多余旧节点时的 diff 比对。
if (i > oldChildrenEnd) {
if (i <= newChildrenEnd) {
const nextPos = newChildrenEnd + 1
const anchor =
nextPos < newChildrenLength
? newChildren[nextPos].el
: parentAnchor
while (i <= newChildrenEnd) {
patch(
null,
normalizeVNode(newChildren[i]),
container,
anchor
)
i++
}
}
}四、旧节点多于新节点时的 diff 比对
// 4. 旧节点多与新节点时的 diff 比对。
else if (i > newChildrenEnd) {
while (i <= oldChildrenEnd) {
unmount(oldChildren[i])
i++
}
}// 4. 旧节点多与新节点时的 diff 比对。
else if (i > newChildrenEnd) {
while (i <= oldChildrenEnd) {
unmount(oldChildren[i])
i++
}
}乱序场景
最长递增子序列的作用
所谓的 diff,其实说白了就是对 一组节点 进行 添加、删除、打补丁 的对应操作。那么除了以上三种操作之外,其实还有最后一种操作方式,那就是 移动。
最长递增子序列的确定,可以帮助我们减少移动的次数
旧节点:1,2,3,4,5,6
新节点:1,3,2,4,6,5
我们可以根据 新节点 生成 递增子序列(非最长)(注意:并不是惟一的),其结果为:
1、3、61、2、4、6- …
我们来分析一下移动的策略,整个移动根据递增子序列的不同,将拥有两种移动策略:
1、3、61、3、6递增序列下:
- 因为
1、3、6的递增已确认,所以它们三个是不需要移动的,那么我们所需要移动的节点无非就是 三 个2、4、5。 - 所以我们需要经过 三次 移动
- 因为
1、2、4、61、2、4、6递增序列下:
- 因为
1、2、4、6的递增已确认,所以它们四个是不需要移动的,那么我们所需要移动的节点无非就是 两个3、5。 - 所以我们需要经过 两次 移动
- 因为
所以由以上分析,我们可知:最长递增子序列的确定,可以帮助我们减少移动的次数
所以,当我们需要进行节点移动时,移动需要事先构建出最长递增子序列,以保证我们的移动方案
求解最长递增子序列
/**
* 获取最长递增子序列下标
* 维基百科:https://en.wikipedia.org/wiki/Longest_increasing_subsequence
*/
function getSequence(arr) {
// 获取一个数组浅拷贝。注意 p 的元素改变并不会影响 arr
// p 是一个最终的回溯数组,它会在最终的 result 回溯中被使用
// 它会在每次 result 发生变化时,记录 result 更新前最后一个索引的值
const p = arr.slice()
// 定义返回值(最长递增子序列下标),因为下标从 0 开始,所以它的初始值为 0
const result = [0]
let i, j, u, v, c
// 当前数组的长度
const len = arr.length
// 对数组中所有的元素进行 for 循环处理,i = 下标
for (i = 0; i < len; i++) {
// 根据下标获取当前对应元素
const arrI = arr[i]
//
if (arrI !== 0) {
// 获取 result 中的最后一个元素,即:当前 result 中保存的最大值的下标
j = result[result.length - 1]
// arr[j] = 当前 result 中所保存的最大值
// arrI = 当前值
// 如果 arr[j] < arrI 。那么就证明,当前存在更大的序列,那么该下标就需要被放入到 result 的最后位置
if (arr[j] < arrI) {
p[i] = j
// 把当前的下标 i 放入到 result 的最后位置
result.push(i)
continue
}
// 二分查找,找到 arr[result[x]] > arrI 的最小 x
u = 0
v = result.length - 1
while (u < v) {
c = (u + v) >> 1
if (arr[result[c]] < arrI) {
u = c + 1
} else {
v = c
}
}
// 最终,经过 while 的二分运算可以计算出:目标下标位 u
// 利用 u 从 result 中获取下标,然后拿到 arr 中对应的值:arr[result[u]]
// 如果:arr[result[u]] > arrI 的,则证明当前 result 中存在的下标 《不是》 递增序列,则需要进行替换
if (arrI < arr[result[u]]) {
if (u > 0) {
p[i] = result[u - 1]
}
// 进行替换,替换为递增序列
result[u] = i
}
}
}
// 重新定义 u。此时:u = result 的长度
u = result.length
// 重新定义 v。此时 v = result 的最后一个元素
v = result[u - 1]
// 自后向前处理 result,利用 p 中所保存的索引值,进行最后的一次回溯
while (u-- > 0) {
result[u] = v
v = p[v]
}
return result
}/**
* 获取最长递增子序列下标
* 维基百科:https://en.wikipedia.org/wiki/Longest_increasing_subsequence
*/
function getSequence(arr) {
// 获取一个数组浅拷贝。注意 p 的元素改变并不会影响 arr
// p 是一个最终的回溯数组,它会在最终的 result 回溯中被使用
// 它会在每次 result 发生变化时,记录 result 更新前最后一个索引的值
const p = arr.slice()
// 定义返回值(最长递增子序列下标),因为下标从 0 开始,所以它的初始值为 0
const result = [0]
let i, j, u, v, c
// 当前数组的长度
const len = arr.length
// 对数组中所有的元素进行 for 循环处理,i = 下标
for (i = 0; i < len; i++) {
// 根据下标获取当前对应元素
const arrI = arr[i]
//
if (arrI !== 0) {
// 获取 result 中的最后一个元素,即:当前 result 中保存的最大值的下标
j = result[result.length - 1]
// arr[j] = 当前 result 中所保存的最大值
// arrI = 当前值
// 如果 arr[j] < arrI 。那么就证明,当前存在更大的序列,那么该下标就需要被放入到 result 的最后位置
if (arr[j] < arrI) {
p[i] = j
// 把当前的下标 i 放入到 result 的最后位置
result.push(i)
continue
}
// 二分查找,找到 arr[result[x]] > arrI 的最小 x
u = 0
v = result.length - 1
while (u < v) {
c = (u + v) >> 1
if (arr[result[c]] < arrI) {
u = c + 1
} else {
v = c
}
}
// 最终,经过 while 的二分运算可以计算出:目标下标位 u
// 利用 u 从 result 中获取下标,然后拿到 arr 中对应的值:arr[result[u]]
// 如果:arr[result[u]] > arrI 的,则证明当前 result 中存在的下标 《不是》 递增序列,则需要进行替换
if (arrI < arr[result[u]]) {
if (u > 0) {
p[i] = result[u - 1]
}
// 进行替换,替换为递增序列
result[u] = i
}
}
}
// 重新定义 u。此时:u = result 的长度
u = result.length
// 重新定义 v。此时 v = result 的最后一个元素
v = result[u - 1]
// 自后向前处理 result,利用 p 中所保存的索引值,进行最后的一次回溯
while (u-- > 0) {
result[u] = v
v = p[v]
}
return result
}第一步:先创建一个空数组result保存索引。遍历nums,将当前项current和result的最后一项对应的值last进行比较。如果当前项大于最后一项,直接往result中新增一项;否则,针对result数组进行二分查找,找到并替换比当前项大的那项。下图示意图中为了方便理解result存放的是nums中的值,实际代码存放的是数组索引。
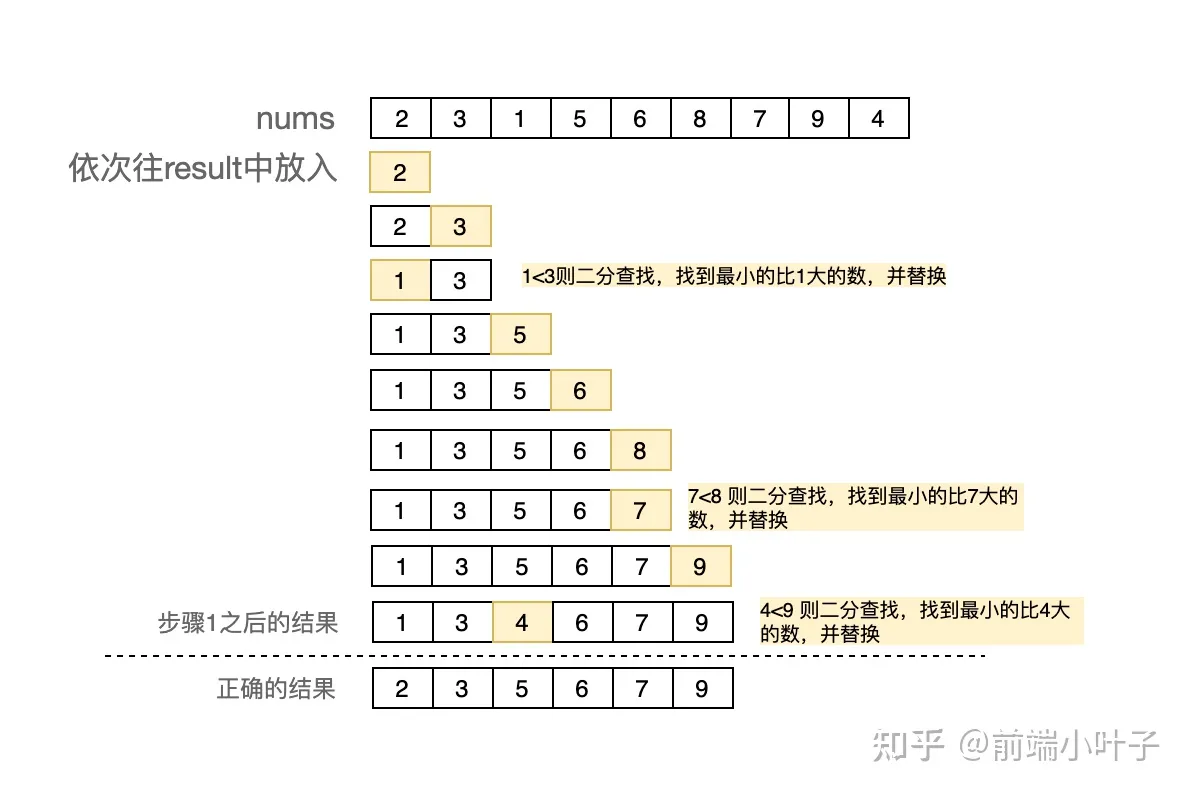
第二步:步骤1得到的结果不正确,要利用p数组修正
使用的前驱节点的概念,需要再创建一个数组preIndexArr(p)。在步骤1往result中新增或者替换新值的时候,同时preIndexArr新增一项,该项为当前项对应的前一项的索引。这样我们有了两个数组:
注意:nums和prevIndex一一对应
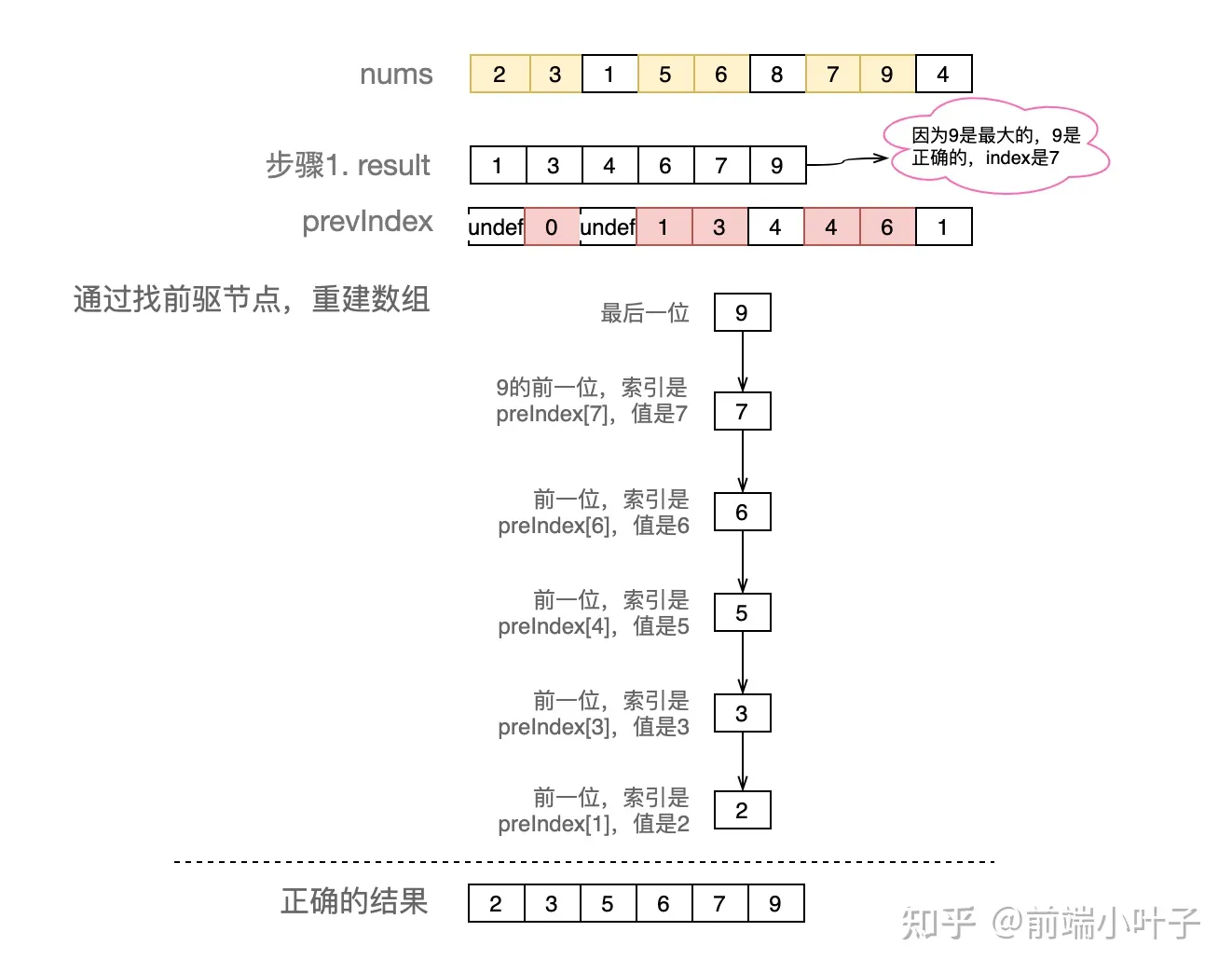
前驱节点的作用:
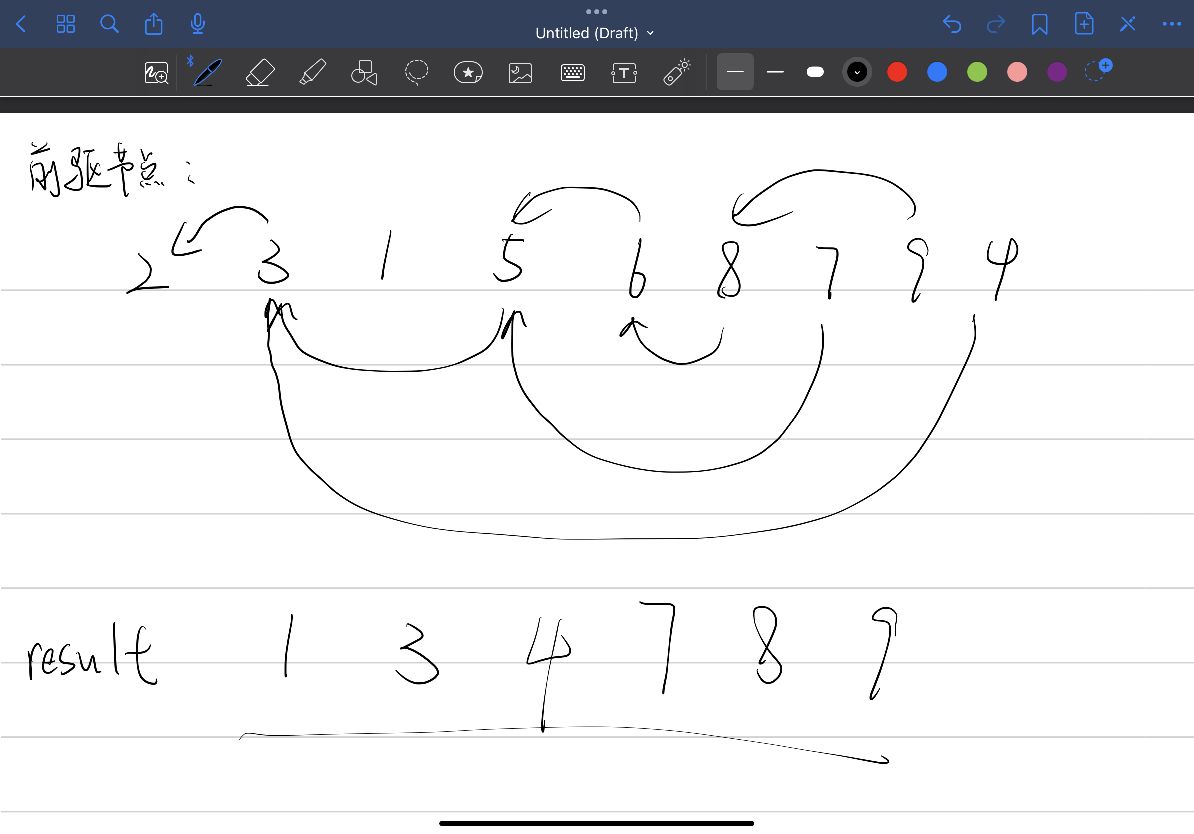
实现
对于
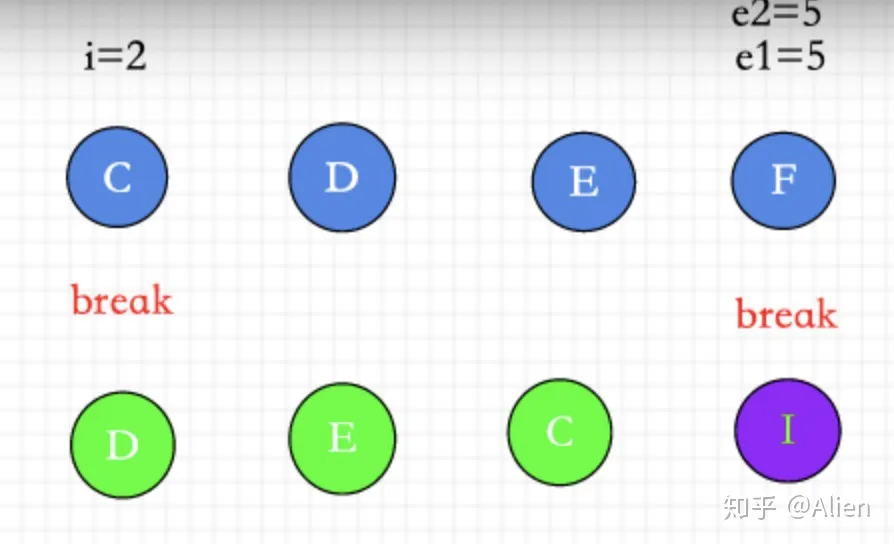
- 创建一个 <key(新节点的 key):index(新节点的位置)> 的 Map 对象 keyToNewIndexMap。通过该对象可知:新的 child(根据 key 判断指定 child) 更新后的位置(根据对应的 index 判断)在哪里
遍历所有新节点把索引和对应的key,存入map keyToNewIndexMap中
keyToNewIndexMap 存放 key -> index 的map
D : 2
E : 3
C : 4
I : 5
- 循环 oldChildren ,并尝试进行 patch(打补丁)或 unmount(删除)旧节点
第一步: 通过老节点的key找到对应新节点的index:开始遍历老的节点,判断有没有key
- 如果存在key通过新节点的keyToNewIndexMap找到与新节点index
- 如果不存在key那么会遍历剩下来的新节点试图找到对应index。
第二步:如果存在index证明有对应的老节点,那么直接复用老节点进行patch,没有找到与老节点对应的新节点,删除当前老节点。
- 在这一步进行patch 或者 unmount 操作
第三步:newIndexToOldIndexMap记录对应新老节点关系。
newIndexToOldIndexMap 此时为 [4,5,3,0]
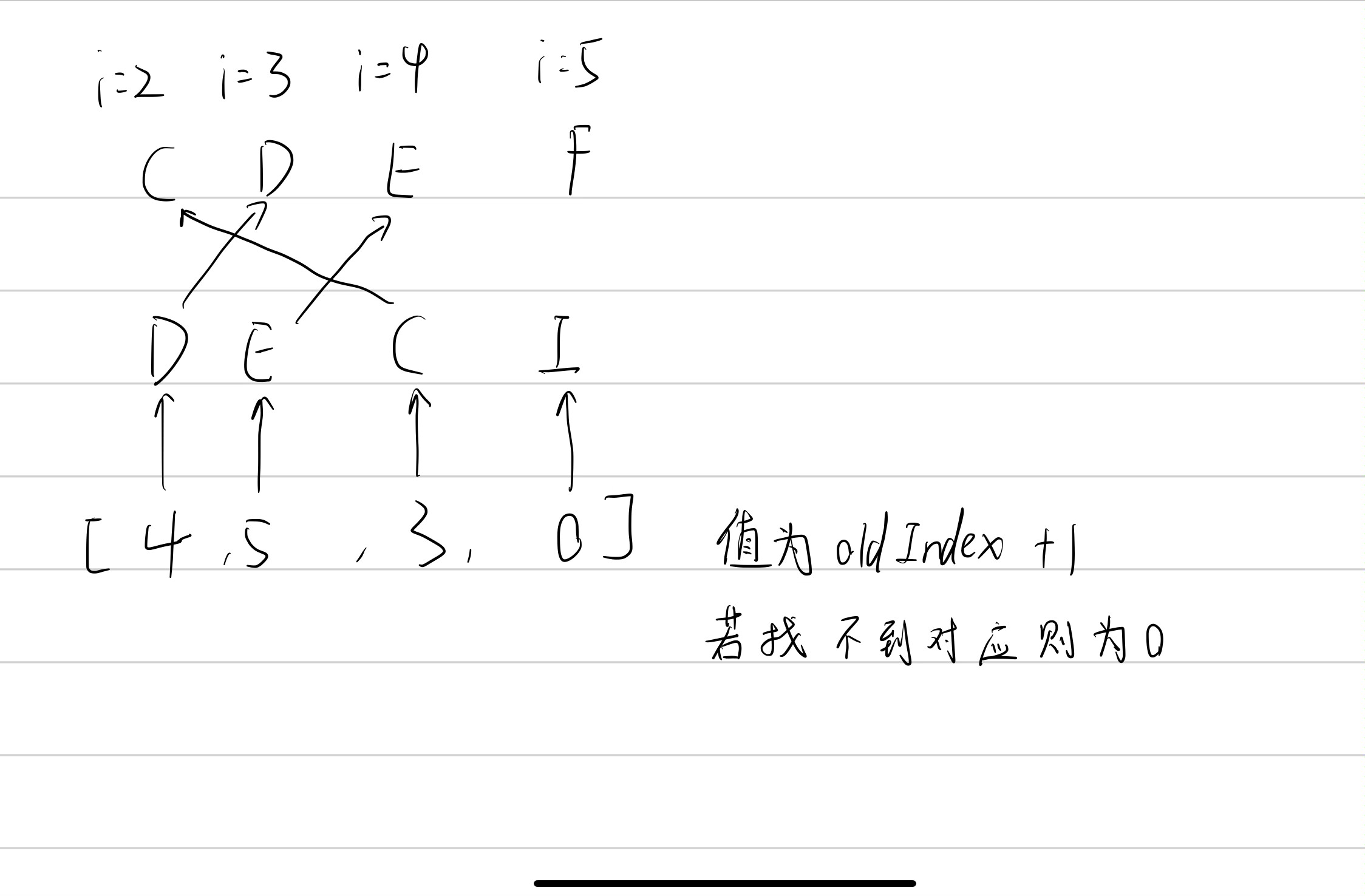
- 针对移动和挂载的处理
虽然已经patch过所有的老节点。可以对于已经发生移动的节点,要怎么真正移动dom元素。(图中节点CDE)
对于新增的节点,(图中节点I)并没有处理,应该怎么处理。
生成 newIndexToOldIndexMap 的最长递增子序列,为 [0,1] ,注意里面放的是 newIndexToOldIndexMap 的下标
